Benjamin Weiner
bjw - at- as.arizona.eduSteward Observatory, University of Arizona

Tully-Fisher B-band relations for integrated linewidths.
This page holds some supporting material for a project that conducted a survey of the kinematics of distant galaxies out to redshifts ~ 1 and greater, using spectra taken by the Team Keck Redshift Survey in the GOODS-N field surrounding the original Hubble Deep Field North.
The survey and its results are described in two papers accepted by the Astrophysical Journal, available from arXiv.org at astro-ph/0609090 and astro-ph/0609091. These papers used data from the TKRS (G. Wirth et al. 2004, AJ, 127, 3121), the GOODS survey (M. Giavalisco et al. 2004, ApJL, 600, L93), and the Hawaii group's imaging of the GOODS-N region (P. Capak et al., 2004, AJ, 127, 180). The faint galaxy data used in this project were all public and we thank these groups for making data and catalogs available in electronic form.
The printed versions of Paper I include shortened versions of the long tables with galaxy magnitudes, restframe magnitudes and colors, kinematic measures (emission-line linewidths, rotation, dispersion), and other properties. You can download the full Tables 2 and 3 in machine-readable form, mrtable2.txt.gz and mrtable3.txt.gz. Please see Paper I for full descriptions of the quantities and their uses and limitations.
You may now also download the spatially-resolved rotation curve data and velocity and dispersion fits for the subset of about 400 galaxies where we fit using the two-dimensional spectroscopic data: ktrs_rc_data.tgz. Please read the file "Readme.rc_data" for the file formats. The various quantities such as rotation velocity and dispersion are described in Paper I. The file "list.goodrc.id" lists the 385 objects (of 464) for which I decided that the ROTCURVE fit was acceptable. DO NOT USE the fitted numbers for the remaining ~79 galaxies with low-quality fits! You'll get garbage.
The least-squares programs page. Part of Paper II, including the Appendix, is devoted to deriving and testing methods for least-squares fitting of linear relations, y=A+Bx , when the data have a large intrinsic scatter about the relation, above the scatter caused by observational error. I distribute some computer programs for least-squares fitting. These programs are developmental, so if you break them in interesting ways, contact me.
Please read the accompanying documentation and the relevant sections of Paper II before using these or any fitting programs blindly, as it is possible to go wrong with any fitting algorithm, especially when your sample has a selection such as a magnitude limit (Paper II gives an example of this in the context of bisector fitting). I also recommend reading the chapter on least-squares model fitting in Numerical Recipes, though keep in mind that these programs are a generalization beyond the methods presented in NR, which do not discuss intrinsic scatter or the effects of selection limits.
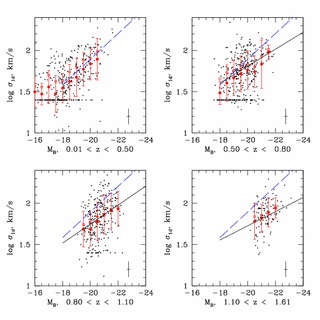
(Figures 1 and 2 from Paper I)
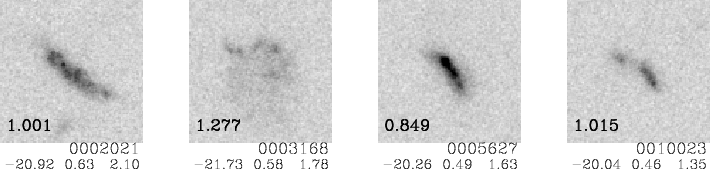
ACS I-band images of four example galaxies with spectra where the slitlets are well aligned with the galaxy major axis. The number in the image panel is redshift; the other numbers are TKRS ID, rest M_B, rest U-B, and log linewidth in km/sec (from the 1-d extracted spectrum). The slitlets for three of the objects run from upper left to lower right, while the slitlet for object 3168 is approximately vertical. (As the next figure shows, we get a good spectrum for 3168 even though it looks awfully low surface brightness in the I-band.)
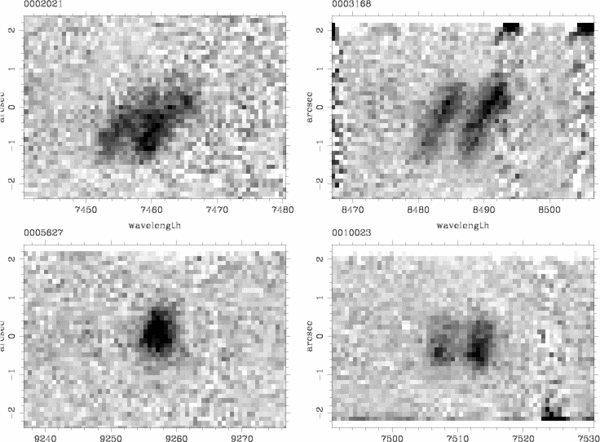
Postage stamps around emission lines from DEIMOS 2-d spectra for the four example galaxies. The first two are strongly rotating and the second two are non-rotating, despite their elongated shapes in the ACS I-band images. The x axis is wavelength and the y axis is distance along the slit. Panels 1, 2, and 4 are of the [O II] 3727 doublet emission line; panel 3 (for object 5627) shows the [O III] 5007 singlet.