Spectral resolution is controlled by pupil size

Since $f_{tel} = D_{tel} N_{tel}$, and $f_{coll} = D_{pupil} N_{tel}$, we can rewrite the equation for resolution as a function of slit width as

$$d\lambda = \frac{dW}{206265''} \frac{D_{tel}}{D_{pupil}} \frac{{\rm cos} \beta}{M_{grating}}.$$

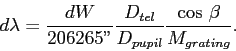
Many factors have dropped out, leaving only telescope and pupil diameters and the lines/mm of the grating (and ${\rm cos} \beta$, which is not very adjustable). This equation expresses a fundamental relation between telescopes and instruments. Everybody wants a bigger aperture telescope, large $D_{tel}$, to gather more light. But in order to get equally high resolution spectra, if we increase $D_{tel}$, we must also increase $D_{pupil}$. ($M_{grating}$ is limited, since a 1200 lines/mm grating already has interline spacing $<1$ micron, close to the wavelengths of the light we are trying to diffract; we can't make a high-quality large grating that is significantly finer.)

Again, this is because increasing the telescope size means we have to scale up the instrument, otherwise a given slit passes a larger range of angles to the grating, and that lowers the resolution. If we tried to get around this by making a faster telescope (smaller $N_{tel}$) with a smaller physical scale $s_{tel}$ at the focal plane, the beam emerging from the focal plane and entering the collimator is faster, so it will make a big pupil anyway.

Note that for given $D_{tel}$, $d\lambda \propto \frac{1}{D_{pupil} M_{grating}}$. $D_{pupil} M_{grating}$ is the total number of lines in the grating, or the total number of interfering elements; this is a common figure of merit for diffracting systems.