Spectrograph resolution

Figure 5: Collimated beams with a small angular separation $d\alpha$, as in the beams from each edge of a slit, are incident from the left on a reflection grating. The outgoing diffracted beams (red and blue) have diffracted angle $\beta$ that depends on wavelength. At each wavelength, the outgoing beams are spread over a small angle $d\beta$ due to the finite size of the slit.

We know the CCD pixel scale in arcsec on the sky, so this lets us calculate the resolution of the spectrograph for a given slit width in arcsec. Here I will neglect an effect called anamorphic demagnification that modifies the slit width as projected on the detector². Let's assume for simplicity that our spectrograph is configured such that $\alpha \geq \beta$, and $d\alpha \geq d\beta$. (In practice, one would not design a spectrograph so that $\alpha=\beta$ exactly, because the grating would also act as a mirror, reflecting zeroth-order light into the camera.) For some slit width $dW$ in arcsec, if the anamorphic factor $d\alpha/d\beta \sim 1$, $dW$ corresponds to a certain number of detector pixels as calculated earlier.

$$dr_{ccd} {\rm (in mm)} = dW / s_{ccd} ,$$

$$dr_{ccd} = \frac{dW}{206265''} f_{tel} \frac{f_{cam}}{f_{coll}},$$

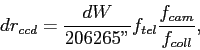
and we had that

$$d\lambda = \frac{dr_{ccd} {\rm cos} \beta}{f_{cam} M_{grating}}.$$

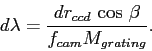
Therefore the delta-wavelength $d\lambda$ for a slit width $dW$ in arcsec is given by

$$d\lambda = \frac{dW}{206265''} \frac{f_{tel}}{f_{coll}}\frac{{\rm cos} \beta}{M_{grating}}.$$

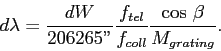
Note that the camera focal length has dropped out here and that $f_{coll}$ is in the denominator, meaning longer collimators give higher resolution for a given slit width. This is because the longer collimator translates a given slit width into a smaller spread of angles, hence a smaller spread of wavelength by the grating.