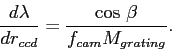![\includegraphics[width=4.5truein]{grating1.eps}](img46.png)
|
![\includegraphics[width=4.5truein]{grating1.eps}](img46.png)
|
A transmission grating deviates light of wavelength ![]() by an angle
by an angle ![]() ,
,
Let's work in first order where ![]() .
For a reflection grating the grating equation is
.
For a reflection grating the grating equation is
where ![]() and
and ![]() are the angles of incident and diffracted rays
with respect to the grating normal, shown in Figure
4. The diffracted beams are shown as red and blue.
Light from a single point source produces one incident collimated beam.
The diffracted beam of a single point source at a single
wavelength (e.g. the blue lines) is still collimated and will be
imaged at a single point on the detector, while the red lines will
be imaged at a different point. The fact that wavelengths are
separated in angle, but each single wavelength stays collimated,
is why we want to have the disperser in the collimated beam.
are the angles of incident and diffracted rays
with respect to the grating normal, shown in Figure
4. The diffracted beams are shown as red and blue.
Light from a single point source produces one incident collimated beam.
The diffracted beam of a single point source at a single
wavelength (e.g. the blue lines) is still collimated and will be
imaged at a single point on the detector, while the red lines will
be imaged at a different point. The fact that wavelengths are
separated in angle, but each single wavelength stays collimated,
is why we want to have the disperser in the collimated beam.
The zeropoint of the diffracted
angle ![]() depends on the incident angle and grating normal,
but the change in
depends on the incident angle and grating normal,
but the change in ![]() with
with ![]() governs the resolution of
the spectrograph.
governs the resolution of
the spectrograph.
We're not directly concerned with the zeropoint of ![]() , assuming
we have tilted the grating so as to get light into the camera,
but with the change in
, assuming
we have tilted the grating so as to get light into the camera,
but with the change in ![]() per wavelength and the resulting
wavelength scale per pixel.
Consider how the camera translates a deviation in angle of the
diffracted beam to a distance on the detector,
per wavelength and the resulting
wavelength scale per pixel.
Consider how the camera translates a deviation in angle of the
diffracted beam to a distance on the detector, ![]() .
For a small deviation in angle,
.
For a small deviation in angle, ![]() , the image moves
, the image moves
By differentiating the grating equation, for a fixed
input angle ![]() ,
,
For typical spectrograph layouts (other than echelles), ![]() is not large and
is not large and
![]() is slightly
is slightly ![]() .
.
This gives the wavelength/physical scale at the CCD: