Reimaging and the scale at the detector

The camera reimages the collimated beams onto the detector/CCD. The camera has to accept the collimated beam so it has

$$D_{cam} = D_{pupil}.$$

In practice, $D_{cam}$ should be slightly greater to avoid vignetting off-axis beams. (This diameter is really the size of the camera's entrance pupil, not the physical size of a lens.) Thus the f-number of the camera is

$$N_{cam} = f_{cam} / D_{pupil} = \frac{N_{tel} f_{cam}}{f_{coll}}.$$

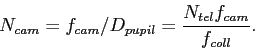
Because the camera focal length is usually fairly short to get demagnification of the focal plane onto a small detector, the camera typically has to be fast (small $N_{cam}$). As drawn in Figure 3, the beam converges with a wider (faster) angle at the detector, compared to the beam delivered by the telescope.

An off-axis beam is reimaged at distance from the detector center of

$$D_{ccd}/2 = \theta_{offaxis} f_{cam}.$$

So this means that

$$D_{ccd} = D_{field} \frac{f_{cam}}{f_{coll}},$$

$$s_{ccd} = s_{tel} \frac{f_{coll}}{f_{cam}},$$

$$s_{ccd} = \frac{206265''}{f_{tel}} \frac{f_{coll}}{f_{cam}}.$$

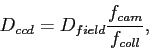
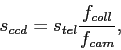
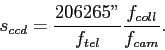
The focal plane and plate scale have been demagnified by the ratio of collimator to camera focal lengths. If the collimator is 3x longer than the camera, the detector can be 3x smaller than the field size in the telescope focal plane. Large telescopes have big focal planes, while detectors are usually smaller, so reimaging systems with demagnification allow us to get a reasonable field of view, and can make the pixel scale a better match to the typical seeing.